📘 🛰️ Special Theory of Relativity — An Academic View

physics
relativity
special relativity
einstein
Step by step, understand the foundations of Einstein’s theory: postulates, transformations, time dilation, twin paradox, mass-energy equivalence, and much more.
Author

Blog do Marcellini

Published

September 25, 2025

← Back to the Special Relativity Reading Guide 🧭 📚 🛰️

← Back to the Physics Reading Guide 🧭 ⚛️

← Back to the Physics Section ⚛️

1 📘 🛰️ Special Theory of Relativity – An Academic View

1.1 Historical Introduction

In 1905, Albert Einstein published the article “On the Electrodynamics of Moving Bodies”, challenging the classical notions of space and time. This new approach — called Special Relativity — is based on two simple yet revolutionary postulates, with surprising consequences for our understanding of the universe.

1.2 Postulates of Special Relativity

  1. Principle of Relativity
    > ℹ️ The laws of physics are the same for all inertial observers (without acceleration).

  2. Constancy of the Speed of Light
    > ⚠️ Light propagates in a vacuum at a constant speed \(c \approx 3{,}00 \times 10^8 \, \text{m/s}\), regardless of the motion of the source or the observer.

1.3 Lorentz Transformations

The Galilean transformation (used in classical mechanics) does not preserve the speed of light. Einstein introduced the Lorentz Transformations, which describe how space and time transform between observers in relative motion:

\[ \boxed{ \begin{aligned} x' &= \gamma (x - vt) \\ t' &= \gamma \left( t - \frac{vx}{c^2} \right) \end{aligned} \quad \text{where } \gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}} } \]

✅ These transformations ensure that the speed of light remains \(c\) in all reference frames.

1.4 Time Dilation: What It Is and How It Works

If a clock is moving relative to an observer, it appears to run slower.

\[ \boxed{ \Delta t = \frac{\Delta t_0}{\sqrt{1 - \frac{v^2}{c^2}}} } \]

  • \(\Delta t_0\): proper time (measured in the rest frame of the event).
  • \(\Delta t\): time measured by an external observer.

ℹ️ At speeds much smaller than \(c\), the effect is negligible — but it becomes significant as \(v\) approaches the speed of light.

1.5 Interactive Graph: Time Dilation

Let’s visualize how time dilates with relative velocity. Assume \(\Delta t_0 = 1\) second.

library(plotly)

velocity <- seq(0, 0.99, by = 0.01)
dilated_time <- 1 / sqrt(1 - velocity^2)

plot_ly(x = ~velocity, y = ~dilated_time,
        type = "scatter", mode = "lines",
        line = list(width = 3)) %>%
  layout(title = "Time Dilation vs Relative Velocity",
         xaxis = list(title = "v/c"),
         yaxis = list(title = "Δt / Δt₀"))

1.6 Graph: Length Contraction

According to Special Relativity, an object in motion relative to an observer will appear shorter along the direction of motion. This is the length contraction.

The formula is:

\[ \boxed{ L = L_0 \sqrt{1 - \frac{v^2}{c^2}} } \]

  • \(L_0\): proper length (measured in the object’s rest frame).
  • \(L\): length measured by an external observer.

Let’s visualize this effect graphically with \(L_0 = 1\) unit:

library(plotly)

v <- seq(0, 0.99, by = 0.01)
L0 <- 1
L <- L0 * sqrt(1 - v^2)

plot_ly(x = ~v, y = ~L, type = "scatter", mode = "lines",
        line = list(width = 3, color = "blue")) %>%
  layout(title = "Length Contraction vs Relative Velocity",
         xaxis = list(title = "v/c"),
         yaxis = list(title = "L / L₀"))

⚠️ Length contraction only occurs in the direction of motion and cannot be perceived by someone in the same reference frame as the object.

1.7 The Twin Paradox

Two twin brothers: one stays on Earth, the other travels at a speed close to \(c\) and then returns.

Result: the traveling twin ages less — time passed more slowly for him.

❗ This is not a contradiction. The traveling twin changes reference frames (acceleration/deceleration), which breaks the symmetry of the system.

This effect has been experimentally confirmed with atomic clocks on airplanes and satellites.

1.8 Comparison with Classical Mechanics

Concept Classical Mechanics (Newton) Special Relativity (Einstein)
Time Absolute Relative to the reference frame
Simultaneity Absolute Relative
Transformations Galilean Lorentz
Speed of light Variable Constant for all observers
Addition of velocities Additive Non-additive
Mass Constant Increases with velocity (relativistic)
Kinetic energy \(\frac{1}{2}mv^2\) \(E = \gamma mc^2 - mc^2\)
Mass–energy equivalence Nonexistent \(E = mc^2\)

1.9 Invariant Interval and Spacetime

One of the central concepts of Special Relativity is the spacetime interval between two events. Just as the Euclidean distance between two points is invariant in classical geometry, the interval between two events is invariant in all inertial reference frames.

The formula for the interval (in 1D) is:

\[ \boxed{ s^2 = c^2 \Delta t^2 - \Delta x^2 } \]

1.9.1 Interpretation of the Interval

Value of \(s^2\) Type of interval Physical meaning
\(s^2 > 0\) Timelike The events can be causally connected.
\(s^2 < 0\) Spacelike The events are too far apart in space for causal influence.
\(s^2 = 0\) Lightlike (null) The events are connected by a light signal.

✅ The interval is invariant: it remains the same in all inertial frames, even if \(\Delta t\) and \(\Delta x\) vary.

1.9.2 Minkowski Spacetime

Special Relativity merges space and time into a single entity: Minkowski spacetime. In it, each event is described by coordinates \((ct, x, y, z)\).

  • The geometry of spacetime is pseudo-Euclidean, with a different signature from Euclidean geometry.
  • This implies that the “square of the distance” between events can be positive, negative, or zero.

1.9.3 Light Cone and Causality

The light cone defines the limits of causality. Events inside the cone can influence or be influenced by the event at the origin. Events outside it are separated by spacelike intervals.

1.9.4 Important Consequences

  • Causal separation between events depends on the invariant interval.
  • The notion of absolute time is no longer valid.
  • Preserving causality requires that no information travel outside the light cone.

1.9.5 Graphical Representation: Light Cone

The figure below shows the light cone in a spacetime diagram:

Light Cone in Spacetime

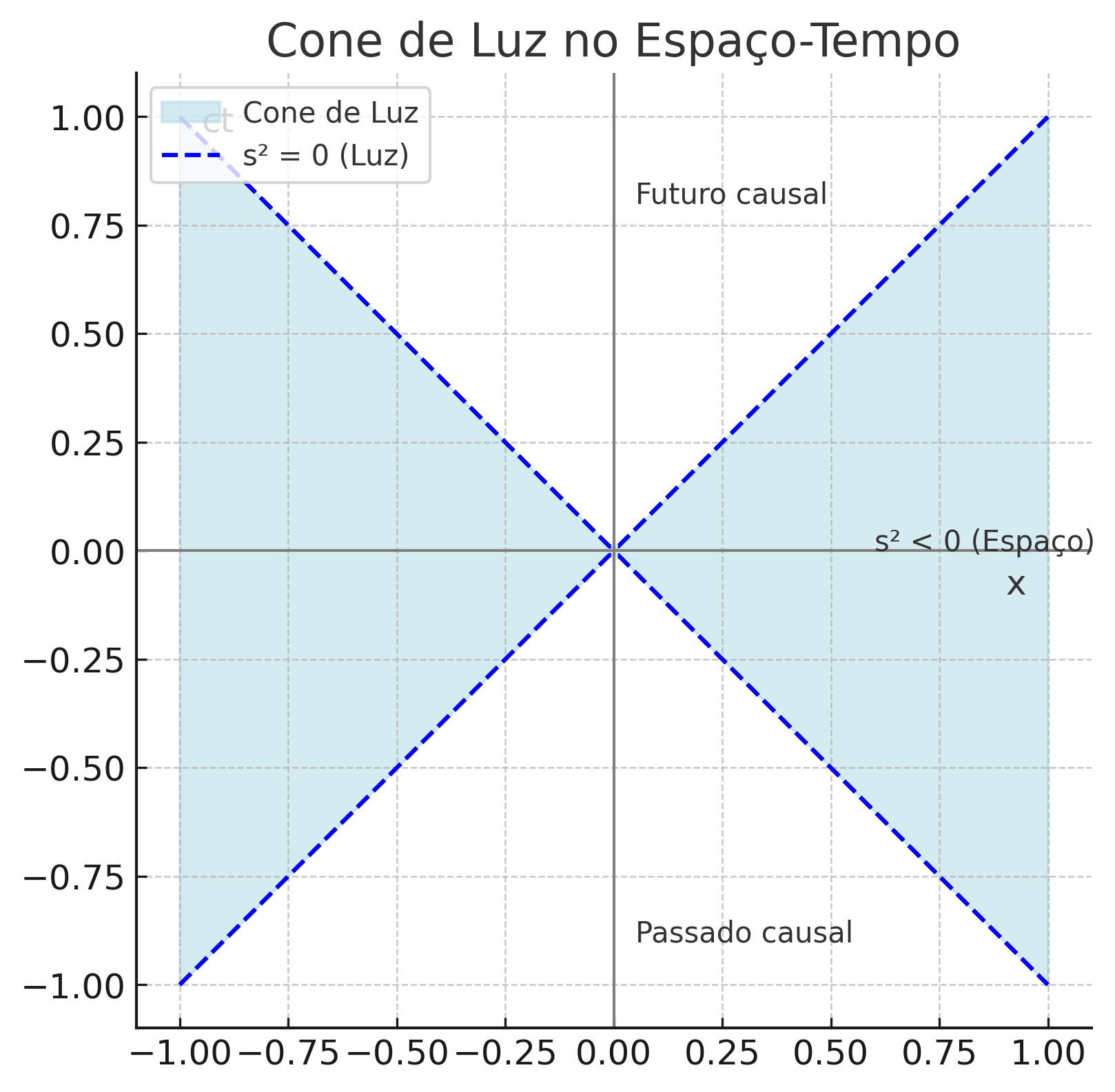
✅ The light cone defines the boundary of causality in Minkowski spacetime.

1.10 Mass–Energy Equivalence and Practical Applications

1.10.1 The Famous Formula

\[ \boxed{E = mc^2} \]

This equation shows that mass is condensed energy.

1.10.2 Applications:

  • ⚛️ Nuclear energy (reactors and bombs);
  • 🌞 Fusion in the Sun;
  • 🛰️ Time corrections in GPS satellites;
  • 🧠 PET scans in medicine;
  • 💥 Particle studies and colliders.

ℹ️ Fun fact: 1 gram of matter fully converted into energy equals 90 trillion joules!

1.11 Conclusion and Final Reflections

Special Relativity transformed our view of the universe. Time and space are interconnected, depend on the observer and velocity. Its accuracy has been experimentally verified in dozens of situations.

✅ It remains essential in modern science and serves as the foundation for broader theories such as General Relativity and Particle Physics.

1.12 ❌ Common Myths about Relativity

Myth Reality
“Nothing can go faster than light” True — in a vacuum. But apparent effects or those in materials may differ.
“Time completely stops at the speed of light” Correct for massive objects (which cannot reach \(c\)).
“Relativity is just a theory” Wrong — it is a theory proven by many experiments.

2 📚 Main Reference:

Resnick, R. (1968). Introduction to Special Relativity. Wiley.

⚠️ In upcoming posts we will explore these concepts in more detail.

3 🧭 📘 🛰️ Reading Guide — Special Relativity

Note

Read this far? Check out the complete reading guide
👉 🧭 📘 🛰️ Reading Guide — Special Relativity

← Back to the Special Relativity Reading Guide 🧭 📚 🛰️

← Back to the Physics Reading Guide 🧭 ⚛️

← Back to the Physics Section ⚛️

🔝 Back to Top

Blog do Marcellini — Exploring Physics with Rigor and Beauty.

Note

Created by Blog do Marcellini with ❤️ and code.