🎓📊 The Normal Distribution — Part 3: Plots, CLT, and Approximate Normality

statistics

normal distribution

courses

central limit theorem

law of large numbers

approximate normality

Visual and theoretical foundations: histograms, Q–Q plots, Law of Large Numbers, and Central Limit Theorem as the basis for approximate normality.

Author

Blog do Marcellini

Published

July 24, 2025

← Course Index · ← Statistics Courses · ← Statistics Section

1 🎓📊 The Normal Distribution — Part 3

In this part, we will address the assessment of normality in real data, both in a visual way (histograms, Q–Q plots) and in a theoretical way (Law of Large Numbers and Central Limit Theorem). Approximate normality is the bridge between descriptive analysis and statistical inference.

Note

📌 Objectives of this post

Identify variables that approximately follow the normal distribution.
Recognize that normality is a key assumption for many statistical methods.
Use plots (histograms, Q–Q plots) to assess the normality of data.
Interpret the results of normality analysis in a practical and applied way.

1.1 🧠 Complements — Understanding Normality in the Real World

In this part, based on Levine et al., Statistics for Managers Using Microsoft Excel, we explore when and how the normal distribution can be used as a valid approximation in real-world contexts.

🎯 Objectives:

Understand under which conditions variables can be treated as approximately normal.
Recognize the importance of normality for methods of statistical inference.
Use practical and graphical criteria to assess the normality of data.

🧠 Let’s deepen our understanding!

1.2 📈 ❓ What Is an Approximately Normal Distribution?

We call approximately normal distributions those variables that, even without following the normal curve exactly, present enough characteristics for statistical methods based on normality to be applied.

👉 Main characteristics:

Bell-shaped form and symmetry around the mean.
Higher concentration of observations close to the mean, with few extreme occurrences.
Most values concentrated within 1 to 2 standard deviations of the mean.

❗ Important notes:

Not every variable needs to be perfectly normal for us to apply statistical tests.
Small asymmetries or irregularities are usually tolerable.
Many real-world distributions are not exactly normal, but rather approximately normal.

📌 Typical examples:

Adult height.
Service times in operations.
Industrial processes under statistical control.

📈 📝 Examples of Distributions: Normal and Non-Normal

✅ Approximately normal variables:

Adult height within the same population.
Service time in standardized operations.
Measurement errors under controlled conditions.

❌ Non-normally distributed variables:

Household income (right-skewed — positive skewness).
Number of children per family (discrete, skewed).
Lifetime of electronic equipment (long right tail).

📌 Note: Some variables can approach normality after transformations, such as logarithm or square root.

📈 📝 Real-World Examples of Approximate Normality

Examples of variables with approximately normal distribution:

Heights of university students.
Phone service times in standardized call centers.
Weights of newborns in hospitals.
Scores on standardized tests (e.g., proficiency exams).
Measurement errors in controlled physics experiments.
Retirement ages in large populations.

❗ Important: Even if the actual distribution is not perfectly normal, a normal approximation is often sufficient for practical applications and statistical inference.

1.3 📈 ❓ What Is a Q–Q Plot?

📊 The Q–Q Plot (Quantile–Quantile Plot) is a chart used to compare the distribution of sample data with a theoretical distribution — usually the normal.

🎯 Objectives:

Assess whether the data approximately follow a normal distribution.
Identify relevant deviations, such as skewness or heavy tails.

🔎 How to interpret:

If the points align close to a diagonal straight line, the data are approximately normal.
Systematic deviations (curvature or tail departures) indicate lack of normality.

📌 Note: The Q–Q Plot is especially useful with large samples, since small imperfections are expected and do not compromise the overall interpretation.

📈 📝 Visual Example — Histogram of a Normal Distribution

👉 Situation:

Sample of 200 adult heights.
Observed mean: \(170\) cm.
Observed standard deviation: \(8\) cm.

📈 Chart:

Histogram of 200 adult heights, with mean 170 and standard deviation 8, showing a bell shape.

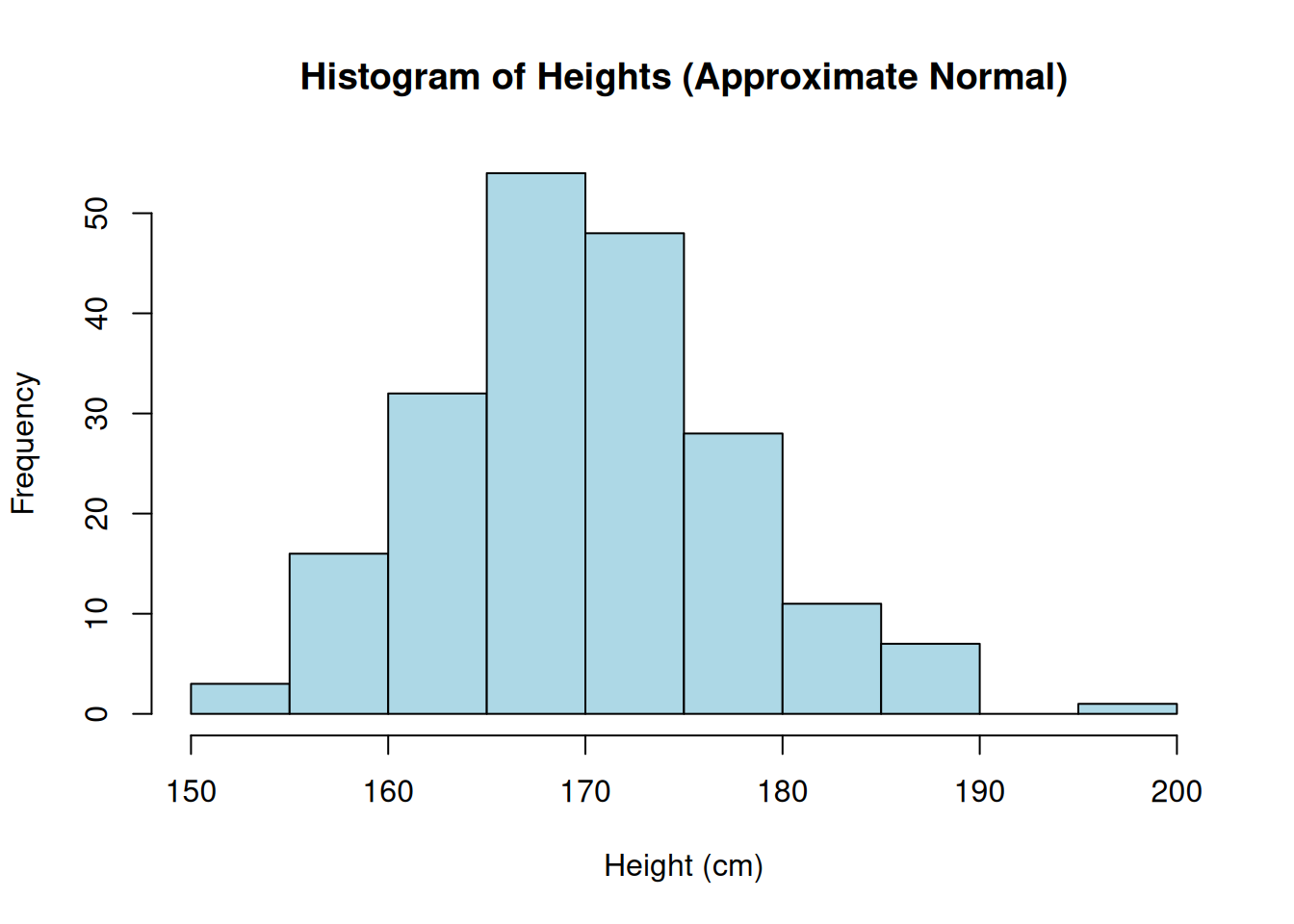
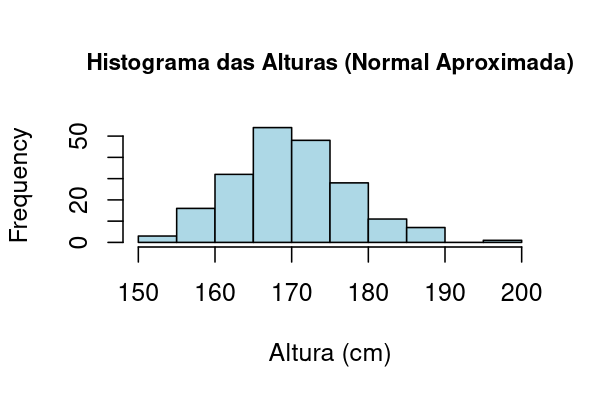
Chart generated in R from 200 simulated observations of \(X \sim \mathcal N(170,\,8^2)\).

🔎 Interpretation: The histogram shows a bell shape, symmetric around the mean. Small variations are expected, but the approximation to the normal distribution is very good.

📈 📝 Visual Example — Q–Q Plot (Levine)

👉 Situation: The same sample of 200 adult heights (\(\mu=170,\; \sigma=8\)) was used to build the Q–Q plot.

📈 Chart:

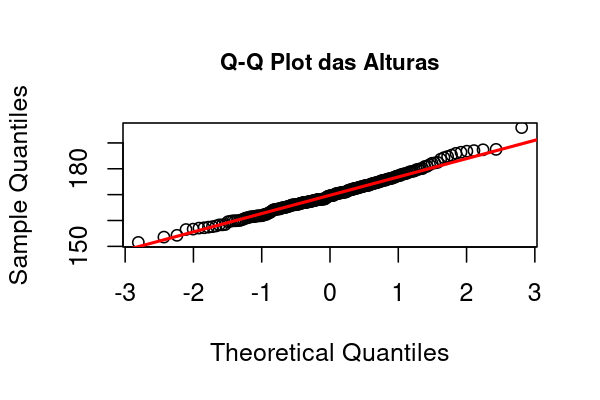
Q–Q Plot of 200 simulated heights from a normal distribution with mean 170 and standard deviation 8.

Chart generated in R with 200 simulated observations of \(X \sim \mathcal N(170,\,8^2)\).

🔎 Interpretation:

When the points align approximately along the straight line, we conclude that the distribution is approximately normal.
Small fluctuations are expected in real samples and do not invalidate the analysis.

Generating Plots in R: Histogram and Q–Q Plot

🎯 Objective: Generate a sample of heights and visualize the histogram and the Q–Q plot directly in RStudio.

# Generate the sample of heights
set.seed(123) # Ensures reproducibility
heights <- rnorm(200, mean = 170, sd = 8)

# Display the Histogram
hist(heights,
breaks = 15,
main = "Histogram of Heights (Approximate Normal)",
xlab = "Height (cm)",
col = "lightblue",
border = "black")

# Display the Q-Q Plot
qqnorm(heights,
main = "Q-Q Plot of Heights")
qqline(heights, col = "red", lwd = 2)

📌 Note: The code generates the plots directly in the RStudio window.

1.4 🧭 Step-by-Step to Generate the Plots in RStudio

🎯 Objective: Build the Histogram and the Q–Q Plot of the height sample using RStudio.

👉 (1) Generate the sample:

Use rnorm() to create random data from a normal distribution.

👉 (2) Build the Histogram:

Use the hist() function to visualize the data distribution.

👉 (3) Build the Q–Q Plot:

Use qqnorm() to create the plot.
Add the reference line with qqline().

❗ Important: Visualize and interpret the plots on screen before applying statistical methods!

🔍 Why visualize plots before the analysis?

Before applying any statistical technique, it is essential to explore the data visually. Plots such as histograms and Q–Q plots help verify fundamental assumptions, like normality, the presence of outliers, and symmetry of the distribution.

Applying statistical tests without this prior check may lead to misleading or statistically invalid conclusions. Visualization allows you to detect patterns, deviations, and anomalies that numbers alone may not reveal—therefore, it is a critical step in the data analysis workflow.

Activity 1: Generating and Interpreting New Plots in RStudio

🎯 Objective: Apply what you’ve learned to generate new plots in RStudio.

🧠 📝 Task:

👉 (1) Generate a new sample of 200 normally distributed observations with:

Mean \(\mu = 160\)
Standard deviation \(\sigma = 5\)

👉 (2) Build:

A Histogram of the generated heights.
A corresponding Q–Q Plot.

👉 (3) Compare visually:

The shape of the new histogram.
The alignment of the points in the Q–Q plot.

💡 Hint: Use the same functions: rnorm(), hist(), qqnorm(), qqline().

🧠 🔎 Answer Key for Activity 1: New Plots Generated in RStudio

🧑‍💻 R Code:

# Generate new sample
set.seed(456) # New seed to vary the data
new_heights <- rnorm(200, mean = 160, sd = 5)

# Histogram
hist(new_heights,
breaks = 15,
main = "Histogram of Heights (New Sample)",
xlab = "Height (cm)",
col = "lightgreen",
border = "black")

# Q-Q Plot
qqnorm(new_heights,
main = "Q-Q Plot of Heights (New Sample)")
qqline(new_heights, col = "blue", lwd = 2)

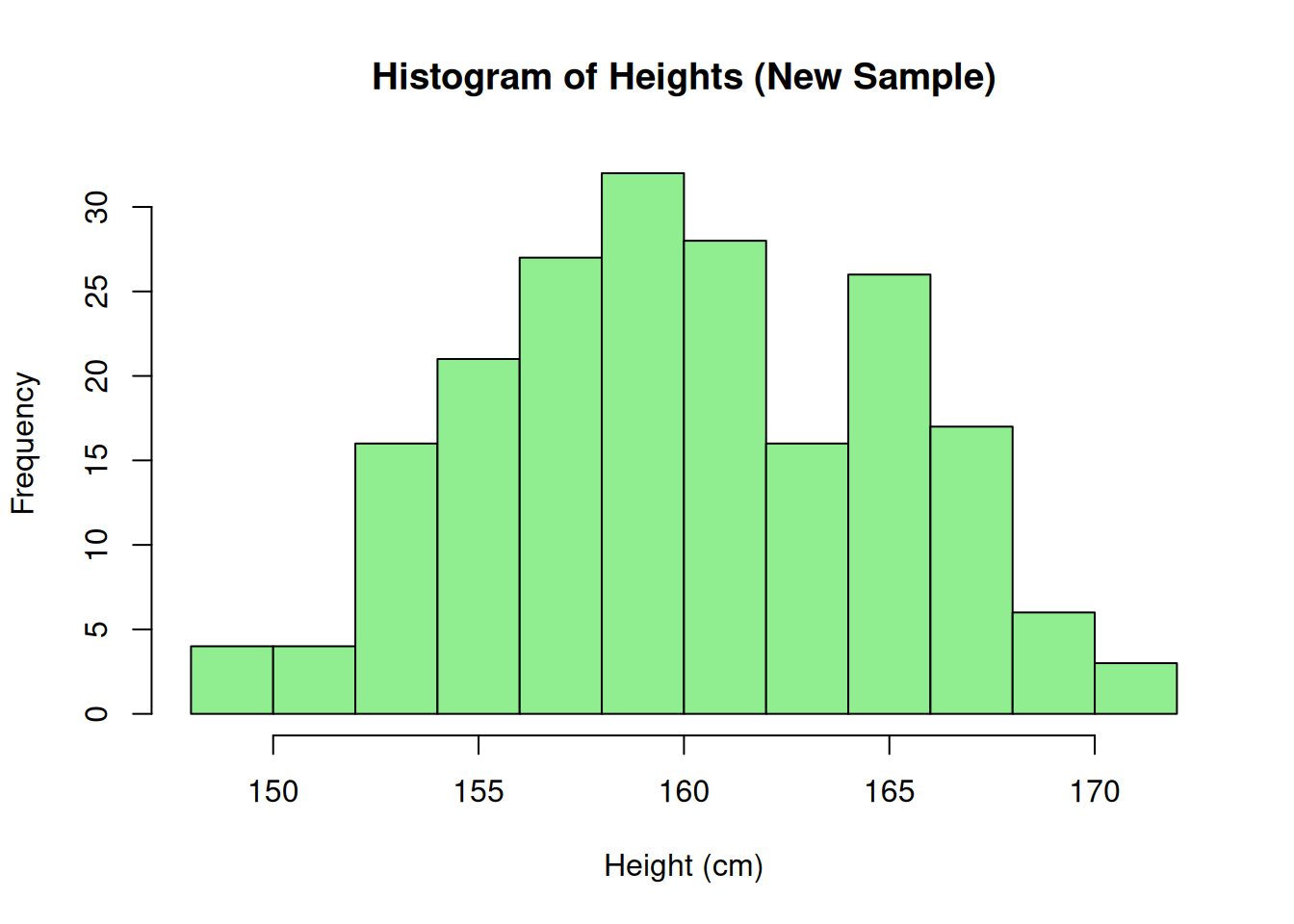
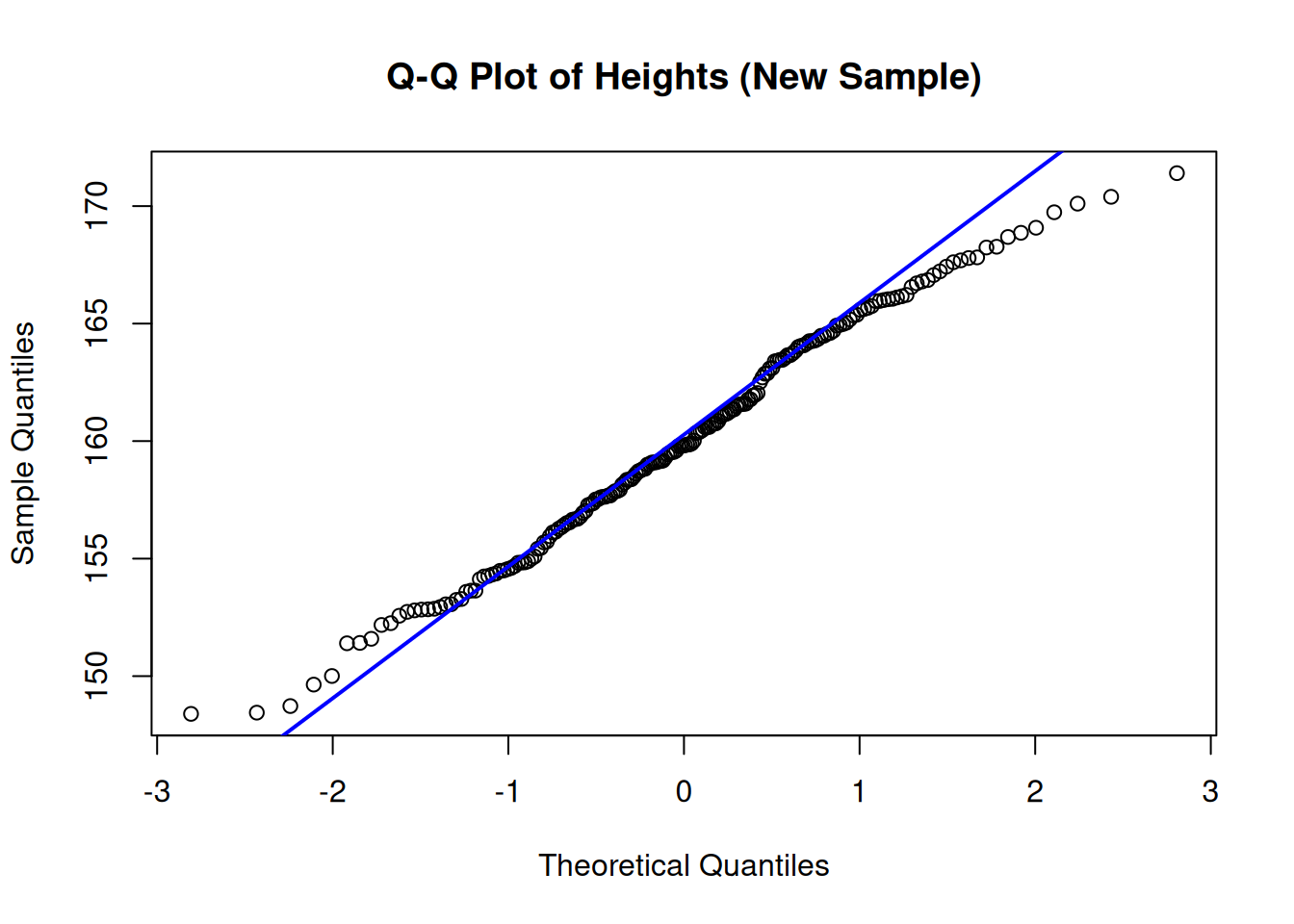
📌 Interpretation: The new data also approximately follow a normal distribution.

1.5 🧭 Step-by-Step to Generate Plots in Excel

🎯 Objective: Build the Histogram and the Q–Q Plot of the height sample using Excel.

📈 Histogram in Excel:

Enter the sample data in a column.
Select the data.
Go to Insert → Statistical Charts → Histogram.
Adjust the number of bins as needed.

📈 Q–Q Plot in Excel:

Sort the sample data (ascending).
Compute the theoretical quantile positions: =NORM.INV((ROW()-0.5)/Total, Mean, StdDev) (Tip: you can obtain Mean and StdDev from the data using AVERAGE(range) and STDEV.S(range).)
Build an XY (Scatter) plot of sample data vs. theoretical quantiles.
Add a linear trendline for reference.

📌 Note: The Q–Q Plot is manual in Excel, but easy to build!

1.6 🧠 Law of Large Numbers (LLN)

Large samples tend to reflect the true population mean.
Variability decreases as we increase the sample size.

📌 Summary: LLN ensures that sample means approach the population mean.

1.7 🧠 Central Limit Theorem (CLT)

The mean of large samples tends to follow a normal distribution.
Regardless of the original distribution!

Conclusion: The CLT is the theoretical basis for using the normal distribution in practice.

1.8 🧠 Variability and the Shape of the Normal Curve

\(\sigma\) small \(\rightarrow\) narrower curve.
\(\sigma\) large \(\rightarrow\) flatter curve.

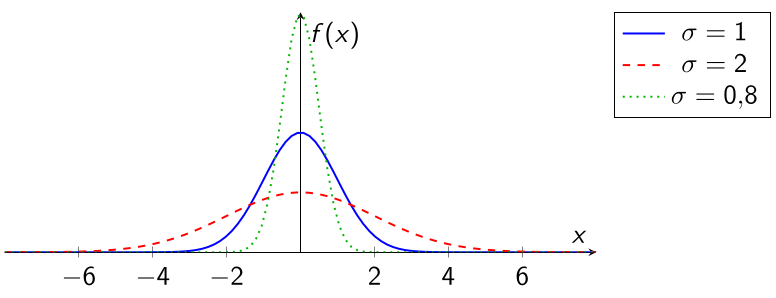
Variability and Shape of the Normal Curve

🧠 📖 Quick Test: True or False?

A normal curve with larger \(\sigma\) is narrower? (T or F)
According to the LLN, small samples already reflect the true mean? (T or F)
The CLT explains the prevalence of normality? (T or F)

🧠 🔎 Answer Key — Quick Test

A normal curve with larger \(\sigma\) is narrower? (F)
According to the LLN, small samples already reflect the true mean? (F)
The CLT explains the prevalence of normality? (T)

📌 Note: Understanding normality is essential to correctly apply statistical tests and make data-driven decisions!

1.9 📌 Conclusion of Part 3: Plots, CLT, and Approximate Normality

In this final part of the course, you learned:

To identify variables that follow an approximately normal distribution.
To recognize that normality is a key assumption for many statistical methods.
To use plots such as histograms and normal probability plots (Q–Q plots) to assess data normality.
To interpret the results of normality analysis in a practical and applied way.

2 📚 References

Important

Schmuller, Joseph. Statistical Analysis with Excel® For Dummies®, 5th ed. Wiley, 2016.
Schmuller, Joseph. Statistical Analysis with R For Dummies® (Portuguese edition), 2nd ed. Alta Books, 2021.
Levine, D. M.; Stephan, D.; Szabat, K. A. Statistics for Managers Using Microsoft Excel, 8th ed. Pearson, 2017.
Morettin, L. G. Estatística Básica: Probabilidade e Inferência, 7th ed. Pearson, 2017.
Morettin, P. A.; Bussab, W. O. Estatística Básica, 10th ed. SaraivaUni, 2023.

3 🔗 Quick Access to Course Parts

🎯 Part 1: Introduction to the Normal Distribution

🎯 Part 2: z-Score and z-Table

🎯 Part 3: Plots, CLT, and Approximate Normality (👉 you are here!)